経済指標と広く知られた統計的手法を使って株価を予測する数多くの研究がこれまでに行われてきました。そして2010年以降のコンピュータの性能の上昇により、機械学習による新しい手法が開発されることになりました。それらのアルゴリズムが、様々な数学的・統計的手法を用いて株式市場を予測できるかどうかを発見することは、興味深いことです。本ブログの目的は、GridDBを使ってデータを抽出し、次に統計的検定を行い、最後に機械学習モデルを構築して、米国の経済指標に基づくS&P500指数の月次価格をモデル化することです。
チュートリアルの概要は以下の通りです。
- 前提条件と環境設定
- データセット概要
- 必要なライブラリのインポート
- データセットの読み込み
- 探索的データ解析と特徴量の選択
- 機械学習モデルの構築と学習
- まとめ
前提条件と環境設定
このチュートリアルは、Windows オペレーティングシステム上の Anaconda Navigator (Python バージョン – 3.8.3) で実施されます。チュートリアルを続ける前に、以下のパッケージがインストールされている必要があります。
-
Pandas
-
NumPy
-
Scikit-learn
-
Matplotlib
-
Statsmodels
-
griddb_python
これらのパッケージをCondaの仮想環境にインストールするには、conda install package-nameを使用します。ターミナルやコマンドプロンプトから直接Pythonを使用する場合は、 pip install package-name でインストールできます。
GridDBのインストール
データセットをロードする際、このチュートリアルでは、GridDB を使用する方法と Pandas を使用する方法の 2 つを取り上げます。Pythonを使用してGridDBにアクセスするためには、以下のパッケージも予めインストールしておく必要があります。
- GridDB C-client
- SWIG (Simplified Wrapper and Interface Generator)
- GridDB Python Client
1. データセット概要
一般的に株式市場のリターン、特にS&P500に最も大きな影響を与えると認識されている指標は、以下のカテゴリーに分類されます:一般的なマクロ経済指標、労働市場指標(失業率や雇用統計)、不動産指標、信用市場指標、金融供給指標、消費者(家計)金融行動指標、商品市場指標などです。
このブログでは、S&P500指数の終値をモデル化しました。ここでは、Google Colab環境で、多くのライブラリを含むPythonプログラミング言語を使用しています。分析期間は1970-01-01 / 2018-04-01で、S&P500指数終値と米国経済指標データの頻度はいずれも月次です。
特徴の説明:
1) SP500 – 各月のS&P500の価格 (単位は米ドル)
2) INTDSRUSM193N – 米国の金利、割引率 (単位: パーセント/年)
3) BUSLOANS – 商工業ローン、全商業銀行 (単位: 10億米ドル)
4) MPRIME – 銀行プライムローン金利 (単位: パーセント)
5) FEDFUNDS – フェデラルファンド実効金利 (フェデラルファンド金利とは、預金取扱機関がフェデラルファンドを夜間に取引する際の金利のこと。) (単位: パーセント)
6) CURRCIR – 流通通貨 (単位: 億ドル)
7) PSAVERT – 個人貯蓄率 (可処分個人所得(DPI)に対する個人貯蓄の割合で、しばしば「個人貯蓄率」と呼ばれる)(単位:百分率)
8) PERMIT – 許可発行地における民間新築住宅許可戸数: 総戸数 (単位: 億ドル)
9) INDPRO – 鉱工業生産。工業生産指数(INDPRO)は、米国の製造業、鉱業、電気・ガス事業者に立地するすべての施設の実質生産高を測定する経済指標)(単位:指数2017=100
10) PMSAVE – 個人貯蓄 (単位: 億ドル)
11) DAUTOSAAR – 自動車小売販売台数: 国内自動車販売台数 (単位: 百万台)
12) UNEMPLOY – 失業水準 (単位: 千人)
13) CPIAUCSL – すべての都市消費者向け消費者物価指数。全米都市平均の全品目(単位:指数 1982-1984=100)。
このデータセットは一般に公開されており、finance.yahoo.com と fred.stlouisfed.org のウェブサイトからダウンロードすることができます。得られたデータは1つのデータセットにまとめられ、欠損値についてもチェック済みです。
2. 必要なライブラリのインポート
import griddb_python as griddb
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline3. データセットの読み込み
それでは、データセットをノートブックに読み込んでみましょう。
3.a GridDBの利用
東芝GridDB™は、IoTやビッグデータに最適な拡張性の高いNoSQLデータベースです。GridDBの理念の根幹は、IoTに最適化された汎用性の高いデータストアの提供、高いスケーラビリティ、高性能なチューニング、高い信頼性の確保にあります。
大量のデータを保存するために、CSVファイルは面倒です。GridDBは、オープンソースで拡張性の高いデータベースであるため、完璧な代替品として機能します。GridDBは、スケーラブルでインメモリなNoSQLデータベースであり、大量のデータを簡単に保存することができます。GridDBを初めて使う場合は、こちらのチュートリアルが参考になります。
すでにデータベースのセットアップが完了していると仮定して、データセットをロードするためのSQLクエリをpythonで記述していきます。
sql_statement = ('SELECT * FROM us_economic_data')
dataset = pd.read_sql_query(sql_statement, cont)変数 cont には、データが格納されているコンテナ情報が格納されていることに注意してください。credit_card_dataset` をコンテナの名前に置き換えてください。詳細は、こちらのチュートリアルGridDBへの読み書きを参照してください。
IoTやビッグデータのユースケースに関して言えば、GridDBはリレーショナルやNoSQLの領域の他のデータベースの中で明らかに際立っています。全体として、GridDBは高可用性とデータ保持を必要とするミッションクリティカルなアプリケーションのために、複数の信頼性機能を提供しています。
3.b Pandasの利用
また、Pandasの read_csv 関数を使用してデータを読み込むこともできます。上記のどちらの方法を使っても、データはpandasのdataframeの形で読み込まれるため、同じ出力になります。
us_economic_data = pd.read_csv('us_economic_data.csv')4. 探索的データ解析と特徴量の選択
データセットが読み込まれたら、今度はそのデータセットを探索してみましょう。head()関数を使って、このデータセットの最初の10行を表示してみます。
us_economic_data.head()df = us_economic_data# Changing the column name and then setting the date as an index od the dataframe
df.rename(columns = {'Unnamed: 0':'date'}, inplace = True)
df['date'] = pd.to_datetime(df['date'])
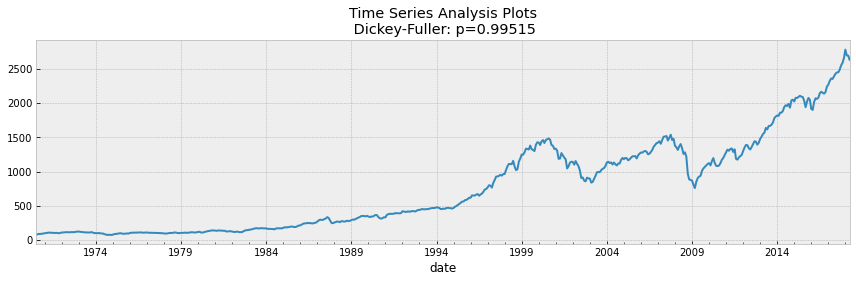
df = df.set_index('date')df.head()S&P500の終値が定常値であるかどうかを判断するためにAugmented Dickey-Fullerを実行しました。その後、終値と各独立変数の間のデータを可視化し、変数間に線形関係があるかどうかを判断し、線形関係がある変数のみを選択しました。
その後、VIF 検定を用いて、独立変数が互いに相関しているかどうかを確認しました。最後に、指標は異なる尺度で測定されているため、z スコア基準でデータを正規化し、正確で信頼性の高いモードになります。
def tsplot(y, figsize=(12, 7), syle='bmh'):
if not isinstance(y, pd.Series):
y = pd.Series(y)
with plt.style.context(style='bmh'):
fig = plt.figure(figsize=figsize)
layout = (2,1)
ts_ax = plt.subplot2grid(layout, (0,0), colspan=2)
y.plot(ax=ts_ax)
p_value = sm.tsa.stattools.adfuller(y)[1]
ts_ax.set_title('Time Series Analysis Plotsn Dickey-Fuller: p={0:.5f}'.format(p_value))
plt.tight_layout()
tsplot(df['SP500'])
data_diff = df['SP500'] - df['SP500'].shift(1)
tsplot(data_diff[1:])Dickey Fuller 検定の仮説の信頼水準を5%とすると,p値 は0.05よりはるかに大きいので,S&P 500は定常的ではないことが分かります。
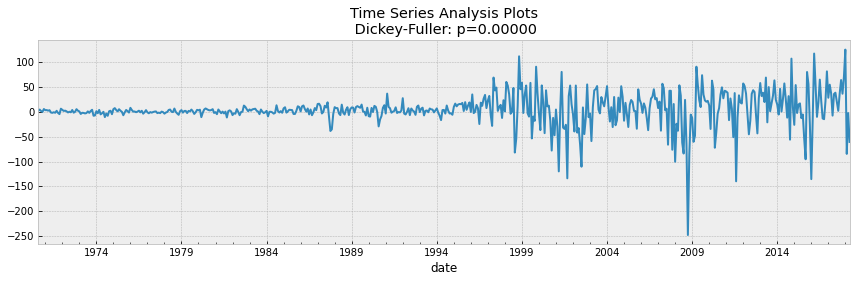
データを定常化するためには、当月価格から前月価格を引いた新しい従属変数を作成する必要がありました。この場合、前述のテストが再計算され、pvalueが0になったので、データは定常であることがわかりました。
次のステップは、独立変数がお互いに相関していないかどうかを見つけることです。この目的のために、VIF 検定が選ばれました。Variance Inflating Factor (VIF) は、回帰モデルでの多重共線性の存在を検定するために使用されます。
df.columnsIndex(['SP500', 'INTDSRUSM193N', 'BUSLOANS', 'MPRIME', 'FEDFUNDS', 'CURRCIR',
'PSAVERT', 'PMSAVE', 'DAUTOSAAR', 'UNEMPLOY', 'INDPRO', 'PERMIT',
'CPIAUCSL'],
dtype='object')
# the independent variables set
X = df[['INTDSRUSM193N', 'BUSLOANS', 'MPRIME', 'FEDFUNDS', 'CURRCIR',
'PSAVERT', 'PMSAVE', 'DAUTOSAAR', 'UNEMPLOY', 'INDPRO', 'PERMIT',
'CPIAUCSL']]
# VIF dataframe
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
print(vif_data) feature VIF
0 INTDSRUSM193N 130.622837
1 BUSLOANS 147.284028
2 MPRIME 399.916868
3 FEDFUNDS 145.507021
4 CURRCIR 112.882897
5 PSAVERT 63.436200
6 PMSAVE 68.862740
7 DAUTOSAAR 60.502647
8 UNEMPLOY 54.757359
9 INDPRO 464.500794
10 PERMIT 34.696174
11 CPIAUCSL 897.072035
表から、各変数のVIFテスト値が10を大きく超えていることがわかります。この場合、最も高いVIF値を持つ指標は除去され、セット全体が再計算されます。これは、10より小さい値を持つすべての変数が残っている限り、行われます。
# the independent variables set
X = df[[ 'FEDFUNDS', 'CURRCIR','PSAVERT', 'PERMIT',]]
# VIF dataframe
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
print(vif_data) feature VIF
0 FEDFUNDS 5.228717
1 CURRCIR 2.532886
2 PSAVERT 8.150866
3 PERMIT 7.039288
その結果、11個はデータが線形であるべきという線形回帰の法則に合致しないことがわかりました。
第2段階の最後は、これらの3つの指標とS&P500指数の価格データを一緒にして、z score基準で正規化することです。
df_new = df[['SP500','FEDFUNDS','CURRCIR','PSAVERT','PERMIT']]df_z_scaled = df_new.copy()
# apply normalization techniques
for column in df_z_scaled.columns:
df_z_scaled[column] = (df_z_scaled[column] -
df_z_scaled[column].mean()) / df_z_scaled[column].std()
# view normalized data
df_z_scaled.head()| date | SP500 | FEDFUNDS | CURRCIR | PSAVERT | PERMIT |
|---|---|---|---|---|---|
| 1970-07-01 | -1.019219 | 0.500923 | -1.065075 | 1.792466 | -0.165538 |
| 1970-08-01 | -1.015924 | 0.351568 | -1.064918 | 1.758546 | 0.002858 |
| 1970-09-01 | -1.008946 | 0.268030 | -1.064531 | 1.588943 | 0.079839 |
| 1970-10-01 | -1.006266 | 0.245247 | -1.064222 | 1.656784 | 0.411821 |
| 1970-11-01 | -1.006401 | 0.093359 | -1.062341 | 1.826387 | 0.262670 |
5. 機械学習モデルの構築
それでは、クレジットカードのデータセットに対して、機械学習モデルを構築し、評価する作業を進めましょう。まず、モデルの「特徴」と「ラベル」を作成し、訓練用とテスト用にサンプルを分割します。テストサンプルはデータセット全体の20%としています。
features = df_z_scaled.drop(columns = ['SP500'], axis = 1)
labels = df_z_scaled[['SP500']]
X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size = 0.2, random_state = 0)print(f"Shape of training data: {X_train.shape}")
print(f"Shape of the training target data: {y_train.shape}")
print(f"Shape of test data: {X_test.shape}")
print(f"Shape of the test target data: {y_test.shape}")Shape of training data: (459, 4)
Shape of the training target data: (459, 1)
Shape of test data: (115, 4)
Shape of the test target data: (115, 1)
第3段階として、ベースラインとなる統計的線形回帰モデルを構築するところからスタートしました。
regr = LinearRegression()
regr.fit(X_train, y_train)
print(regr.score(X_test, y_test))0.9351836569209164
coefficients = pd.concat([pd.DataFrame(X.columns),pd.DataFrame(np.transpose(regr.coef_))], axis = 1)
coefficients| 0 | 0 | |
|---|---|---|
| 0 | FEDFUNDS | 0.083735 |
| 1 | CURRCIR | 1.003270 |
| 2 | PSAVERT | -0.087568 |
| 3 | PERMIT | 0.116120 |
流通貨幣量は最も高い係数を持ち、これはモデルへの影響が大きいことを意味します。
学習データに対してモデルの適合が完了したら、モデルの性能を評価するためにテストセットに対して予測を行うことができます。予測値は predicted に格納されます。
評価指標:
1) 決定係数(R^2)。これはデータに対するモデルの信頼度を示す最も重要な指標であり、回帰モデルの説明には必ず必要です。
2) 平均二乗誤差(MSE)。この値は実際の値と予測値の間の二乗平均平方根誤差を測定します。
y_pred = regr.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print("MSE: ", mse)
print("RMSE: ", mse*(1/2.0))
r2 = r2_score(y_test, y_pred)
print('r2 score for Random Forest model is', r2)MSE: 0.06275016232171571
RMSE: 0.031375081160857854
r2 score for Random Forest model is 0.9351836569209164
ランダムフォレスト回帰は、樹木のアンサンブル学習の手法です。木に基づく予測は多くの予測を考慮するためより正確です。これは平均値を用いるためです。これらのアルゴリズムはより安定しています。なぜなら、データセットに何らかの変更があった場合、1つの木には影響を与えるが、木の森には影響を与えないからです。
rfr = RandomForestRegressor()
rfr.fit(X_train, y_train)
score = rfr.score(X_train, y_train)
print("R-squared:", score)R-squared: 0.9993703842202256
ypred = rfr.predict(X_test)
mse = mean_squared_error(y_test, ypred)
print("MSE: ", mse)
print("RMSE: ", mse*(1/2.0))
r2 = r2_score(y_test, ypred)
print('r2 score for Random Forest model is', r2)MSE: 0.0031918233911353254
RMSE: 0.0015959116955676627
r2 score for Random Forest model is 0.9967030791266005
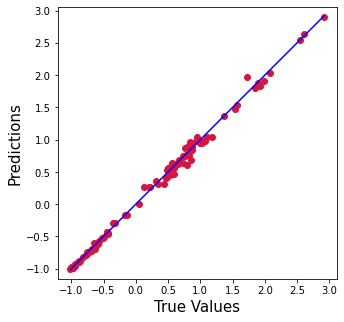
plt.figure(figsize=(5,5))
plt.scatter(y_test['SP500'].values, ypred, c='crimson')
p1 = max(max(ypred), max(y_test['SP500'].values))
p2 = min(min(ypred), min(y_test['SP500'].values))
plt.plot([p1, p2], [p1, p2], 'b-')
plt.xlabel('True Values', fontsize=15)
plt.ylabel('Predictions', fontsize=15)
plt.axis('equal')
plt.show()ベースラインとRandom Forestモデルの比較
Random Forestモデルは、最も高いR2と最も低いエラーレートを提供するため、より優れた機械学習モデルであることがわかりました。統計的線形回帰モデルは6 %改善され、エラーレートは20倍減少しました。
6. まとめ
このチュートリアルでは、株式市場、特にS&P500指数に最も大きな影響を与える可能性のある13の指標を特定しました。データを読み込む方法として、(1) GridDB と (2) Pandas の2つの方法を検討しました。GridDBは、オープンソースで拡張性が高いため、大規模なデータセットを扱う場合、ノートブックにデータを取り込むための優れた代替手段となります。GridDBを今すぐダウンロードしてください。
If you have any questions about the blog, please create a Stack Overflow post here https://stackoverflow.com/questions/ask?tags=griddb .
Make sure that you use the “griddb” tag so our engineers can quickly reply to your questions.